Castings in Java are considered a bad practice.
Java’s strong static typing is a powerful compile-time safeguard. It checks that every method receives and returns objects with the features they are supposed to have. It makes sure that everything is well assembled.
Castings open a backdoor in this mechanism by allowing unchecked type transformations between classes involved in an inheritance. Although castings hardly have any impact in performance, they may lead to runtime errors, which in part defeats the very purpose of strong static typing.
It is commonly agreed that a repeated use of castings denotes a bad design. However, there are some cases in which avoiding them is far from obvious. One of these cases is having several subclasses inheriting from a superclass whose methods have argument or return types referring to the subclasses themselves:
public class A {
public A method(A other) {...};
}
public class B extends A {
@Override
public B method(B other) {...}; // !!
}
Is it possible to avoid castings here?
A Tale of Two Castings
Suppose that we have found a really good algorithm to find
long chains of elements. It takes elements from a Set<T>,
and for any two of them, it needs to know if they may be chained.
With this information, it efficiently builds long chains of elements.
For instance, it may find knight tours in a chessboard
or it could create lists of words that change only one letter in each step:
PASS
PAST
CAST
COST
MOST
LOST
LOFT
...
The skeleton of our Chainer would be something like this:
public class Chainer<T> {
final Set<T> items;
public Chainer(final Set<T> items) {
this.items = items;
}
public List<T> longChain() {
// try to build a very long chain
//
// during the process, lots of pairs of elements are taken from items;
// for each pair we need to check whether they may be chained or not
};
public List<T> joiningChain(T a, T b) {
// try to build a chain joining a and b - again, pairs of elements
// are checked for "chainability"
};
}
The type T does not provide the logic of chainable elements.
So we build a Chainable interface to provide this logic:
// Chainer.java
public class Chainer<T extends Chainable> { /* ... */ }
// Chainable.java
public interface Chainable {
public boolean mayBeChainedTo(Chainable other);
}
// CKnight.java
public class CKnight implements Chainable {
public boolean mayBeChainedTo(Chainable other) { /* ... */ }
}
// CString.java
public class CString implements Chainable {
public boolean mayBeChainedTo(Chainable other) { /* ... */ }
}
You see, we already have two examples of Chainable: chessboard squares
and strings. Two squares may be chained if connected by a single knight jump,
and two strings may be chained if only one letter differs. The logic itself
is not very hard to implement. However, one may perceive a little subtlety
with the types.
// CKnight.java
public boolean mayBeChainedTo(Chainable other) {
CKnight k = (CKnight)other;
// ...
}
The right thing would be to compare a CKnight with another CKnight,
but the inherited method requires comparing with a Chainable.
This forces us to begin the comparison with a downcasting.
But castings make programmers sad

Another possibility would be to provide a BiPredicate<T,T> to the Chainer
public class Chainer<T> {
final Set<T> items;
final BiPredicate<T,T> areChainable;
// ...
}
but this would defeat our aim to encapsulate the behavior in the type itself.
Anoter example, this one a bit more complicated: imagine that we are building an applet that deals with 2-D geometric elements: points, curves, polygons, circles, splines, …
One may conceive different approaches to model 2-D regions. We could think of a numerical approach, where we would model the region using some sort of bitmap, or we could go towards a more analytic approach, keeping track of the atomic components. And perhaps both approaches are useful and can be used simultaneously (one to draw stuff on the screen and the other to perform accurate calculations).
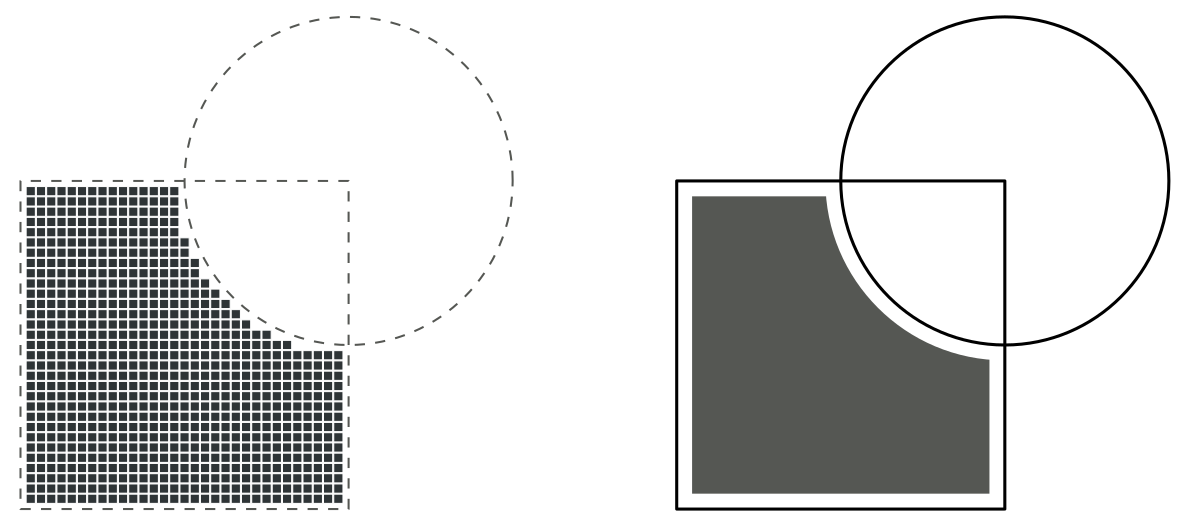
All the approaches would need to implement a similar set of
algebraic operations including union, intersection, complement and difference.
Some of these operations may be computed in terms of others. This way we create
the AlgebraicSet interface. The interface provides a default implementation
for intersection and diff, calculated using the other two operations
(union and complement).
public interface AlgebraicSet {
public AlgebraicSet union(AlgebraicSet other);
public AlgebraicSet complement();
// --------
public default AlgebraicSet intersection(AlgebraicSet other) {
return this.complement().union(other.complement()).complement();
}
public default AlgebraicSet diff(AlgebraicSet other) {
return this.intersection(other.complement());
}
}
Cool!! Let’s now implement BitMap.
public class BitMap extends AlgebraicSet {
public BitMap(/* ... */) {
// perhaps it could be implemented as some sort of double array of booleans?
}
public BitMap union(AlgebraicSet other) {
BitMap bitmapOther = (BitMap)other;
// bitwise AND
return new BitMap(/* ... */);
}
public BitMap complement() {
// bitwise NOT
return new BitMap(/* ... */);
}
}
Did you notice?

And this time it’s slightly worse: there is a downcasting for the argument type
much like in Chainable, but there’s also a difference in the return type.
The initial methods to be implemented were
AlgebraicSet union(AlgebraicSet other) and AlgebraicSet complement();
Java allows tweaking the return type with BitMap union(AlgebraicSet other)
and BitMap complement(), but it’s still ugly nevertheless.
Let’s hope better luck for our symbolic approach in Shape:
public abstract class Shape implements AlgebraicSet {
// union and complement in terms of certain subclases
public Shape union(AlgebraicSet other) {
Shape symbOther = (Shape)other; // Casting :/
return new Union(this, symbOther);
}
public Shape complement() {
return new Complement(this);
}
// checking whether a region contains a point
// BitMap does not implement it because it's not accurate enough
public abstract boolean contains(double x, double y);
// --------
public static class Union extends Shape {
protected Shape a;
protected Shape b;
public Union(Shape a, Shape b) {
this.a = a;
this.b = b;
}
public boolean contains(double x, double y) {
return a.contains(x, y) || b.contains(x, y);
}
}
public static class Complement extends Shape {
protected Shape a;
public Complement(Shape a) {
this.a = a;
}
public boolean contains(double x, double y) {
return !a.contains(x, y);
}
}
// a couple of basic shapes
public static class Rectangle extends Shape {
protected double x0;
protected double x1;
protected double y0;
protected double y1;
public Rectangle(double x0, double x1, double y0, double y1) {
this.x0 = x0;
this.x1 = x1;
this.y0 = y0;
this.y1 = y1;
}
public boolean contains(double x, double y) {
return x0 <= x && x <= x1 && y0 <= y && y <= y1;
}
}
public static class Circle extends Shape {
protected double xc;
protected double yc;
protected double r;
public Circle(double xc, double yc, double r) {
this.xc = xc;
this.yc = yc;
this.r = r;
}
public boolean contains(double x, double y) {
return (x-xc)*(x-xc) + (y-yc)*(y-yc) <= r*r;
}
}
}
Ok. No problem so far. Let’s check that everything’s peachy.
new Rectangle(-1,1,-1,1).union(new Circle(1,1,1)).contains(0,0);
// OK --> true
Great.
new Rectangle(-1,1,-1,1).diff(new Circle(1,1,1)).contains(0,0);
// KO --> The method contains(int, int) is undefined for the type AlgebraicSet
What??!! The method diff was not implemented in Shape,
but in AlgebraicSet, and therefore its return type is AlgebraicSet.
Although semantically equivalent, union and diff work with different types.
So each time we use diff we have to perform another downcasting
((Shape)new Rectangle(-1,1,-1,1).diff(new Circle(1,1,1))).contains(0,0);
// (╯°□°)╯︵ ┻━┻
and this is too much. We need to find a better solution.
A wannabe type
In both examples, Chainable and AlgebraicSet, the problem is more or less
the same: we want to build certain logic that will be inherited by
multiple subclasses, and we need to have the current subclass type
in the implementation.
How can we do this? Imagine that we have a type Base that will be extended
by some type T; inside Base we want to refer to T so… why not?
We introduce T as a type parameter.
class Base<T> // Base will eventually become T
Now we may use T to define argument and return types. But, on the other hand,
T cannot be anything, it has to extend Base.
class Base<T extends Base>
But Base is no longer a raw type; it needs to be told about T.
class Base<T extends Base<T>>
What’s going on here? Is this a circular definition? Nope,
it’s perfect Java syntax. You can impose type predicates on the parameters.
If you find some T satistying the predicate, you’ll be able to instantiate
a Base<T>. If the predicate is impossible to fulfill, then you won’t be able
to instantiate a Base<T>, although everything will compile fine.
Suppose that Derived is to extend Base
class Derived extends Base<Derived>
Look, it works!! Base<Derived> is ok because Derived extends Base<Derived>
satisfies the condition T extends Base<T>. And now Derived inherits
all the logic in Base with all the T replaced by Derived.
Think of Base<T> as being in mid-metamorphosis towards T:
that’s why Derived extends Base<Derived>, because Base<Derived>
was already prepared to be transformed in Derived.
How does this approach translate in our previous examples?
// Chainable.java
public interface Chainable<C extends Chainable<C>> {
public boolean mayBeChainedTo(C other);
}
// CKnight.java
public class CKnight implements Chainable<CKnight> {
public boolean mayBeChainedTo(CKnight other) { /* ... */ };
}
// CString.java
public class CString implements Chainable<CString> {
public boolean mayBeChainedTo(CString other) { /* ... */ };
}
// Chainer.java
public class Chainer<C extends Chainable<C>> {
final Set<C> items;
public Chainer(final Set<C> items) {
this.items = items;
}
public List<C> longChain() { /* ... */ };
public List<C> joiningChain(C a, C b) { /* ... */ };
}
Did you see? No castings!
// AlgebraicSet.java
public interface AlgebraicSet<A extends AlgebraicSet<A>> {
public A union(A other);
public A complement();
// --------
public default A intersection(A other) {
return this.complement().union(other.complement()).complement();
}
public default A diff(A other) {
return this.intersection(other.complement());
}
}
// BitMap.java
public class BitMap implements AlgebraicSet<BitMap> {
// ...
public BitMap union(BitMap other) {
// bitwise AND
return new BitMap(/* ... */);
}
public BitMap complement() {
// bitwise NOT
return new BitMap(/* ... */);
}
}
// Shape.java
public abstract class Shape implements AlgebraicSet<Shape> {
public Shape union(Shape other) {
return new Union(this, other);
}
public Shape complement() {
return new Complement(this);
}
public abstract boolean contains(double x, double y);
// ...
}
Fabulous! Our types match perfectly!
new Rectangle(-1,1,-1,1).union(new Circle(1,1,1)).contains(0,0); // OK
new Rectangle(-1,1,-1,1).diff(new Circle(1,1,1)).contains(0,0); // OK
Strange? Witchcraft? Well, you’d be surprised to know that this technique
is already being used in the core of Java: the keyword enum
public enum Suit {HEART, DIAMOND, CLUB, SPADE};
is indeed syntactic sugar of
a class Enum
that uses this “recursive definition”
class Enum<E extends Enum<E>> {
...
}
class Suit extends Enum<Suit> {
public static final Suit HEART;
public static final Suit DIAMOND;
public static final Suit CLUB;
public static final Suit SPADE;
// ...
}
This makes sense because all our enum have common properties
but we want each subclass to be compared to members of the same subclass,
much like with the Chainable elements. Yes, sometimes you have to reason
in terms of your subclass types.
Polymorphic Fixpoint
We’re very happy with our trick and ready to move on. Let’s add another common
set operation to AlgebraicSet: the symmetric difference.
public default A symDiff(A other) {
return this.diff(other).union(other.diff(this));
}
// The method diff(A) in the type AlgebraicSet<A>
// is not applicable for the arguments (AlgebraicSet<A>)
Yikes!! Since this method is implemented in the parent class,
this refers to the parent class, and not to the child class.
But we need this to be the child class. What can we do?
// Base.java
abstract class Base<T extends Base<T>> {
abstract public T getChild();
}
// Derived.java
class Derived extends Base<Derived> {
public Derived getChild() { return this; }
}
Looks good! To formalize this process we’ll create a Fixpoint interface
that will be implemented by all the classes using this
polymorphic fixpoint trick:
public interface Fixpoint<X extends Fixpoint<X>> {
public X fixpoint();
}
Let’s introduce Fixpoint in Chainable…
// Chainable.java
public interface Chainable<C extends Chainable<C>> extends Fixpoint<C>
// CKnight.java
public CKnight fixpoint() { return this; }
// CString.java
public CString fixpoint() { return this; }
… and in AlgebraicSet:
// AlgebraicSet.java
public interface AlgebraicSet<A extends AlgebraicSet<A>> extends Fixpoint<A> {
public A union(A other);
public A complement();
// --------
public default A intersection(A other) {
return fixpoint().complement().union(other.complement()).complement();
}
public default A diff(A other) {
return fixpoint().intersection(other.complement());
}
public default A symDiff(A other) {
return fixpoint().diff(other).union(other.diff(fixpoint()));
}
}
// BitMap.java
public BitMap fixpoint() { return this; }
// Shape.java
public Shape fixpoint() { return this; }
Did you see? In AlgebraicSet we are now using fixpoint(), of type A,
instead of this, of type AlgebraicSet<A>. Same happens with Chainable.
Why “fixpoint”? Because we’re asking each instance to “evolve” to its
“more developed version”, but in the final subclases this evolution
is the identity, and thus the return this;. And why “polymorphic”?
Well, becuase this “more developed version” takes lots of different forms
indeed.
Altogether, we have built the following hierarchy of classes/interfaces:
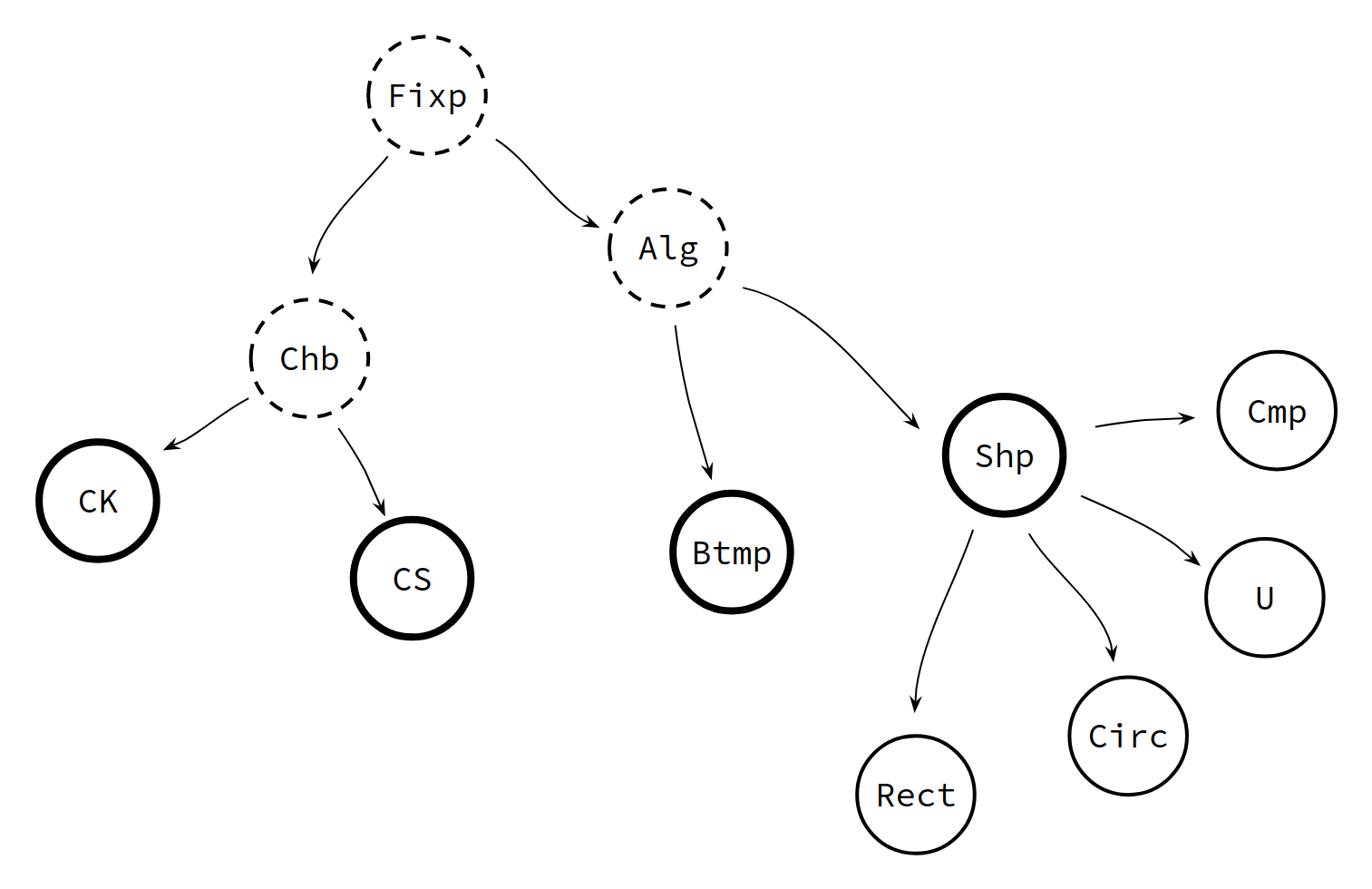
The dashed objects incorporate the polymorphic fixpoint trick in their
type definition and cannot be instantiated until the thick objects
implement fixpoint() { return this; } and no longer receive a type parameter.
From this moment on, type inheritance is completely standard.
Now we can let our imagination fly and come up with all kinds of fancy stuff, like for example a fluent logger able to write the status of an object at any time
public interface Logger<L extends Logger<L>> extends Fixpoint<L> {
default public L log() {
System.out.println(repr());
return fixpoint();
}
public String repr();
}
// BitMap.java
public class BitMap implements AlgebraicSet<BitMap>, Logger<BitMap> {
// ...
public String repr() { /* ... */ }
}
// some other file
new BitMap(/* ... */).log().union(new BitMap(/* ... */));
Wrapping up
To sum up: the polymorphic fixpoint trick is very useful to avoid castings in situations where a behavior is to be extended by several different implementations but needs to refer to the implementations themselves.